Voici une magnifique animation en musique sur la vie interne d’une cellule, créée par des chercheurs de l’université de Harvard en collaboration avec un studio d’animation.

Pour une petite description (en français) de ce qui se passe, on peut voir sur ce blog.
Pour une version plus complète de la vidéo avec un maximum d’explications (en anglais) pour l’enseignement : voir le site d’Harvard.

A voir absolument !

Sauriez-vous faire la différence entre 0.002 cents et 0.002 dollars ?
Apparemment, certains téléopérateurs ne savent pas. Le problème, c’est qu’il y a quand même une grande différence entre une facture de 71.78 $ et une facture de 0.7178 $.

Le brave Georges passe plus de 20 minutes à tenter d’expliquer cela à 2 opérateurs, en vain.
Comment auriez-vous fait pour expliquer que 0.002 cents que multiplient 35 893 kB ne font pas 71.78 $ ?

Peut-être en faisant comme lui :

G : « Y a-t-il une différence entre 0.002 $ et 0.002 cents ? »
V : « ………… 0.002 $ et 0.002 cents ? ………..  »
G : « Y a-t-il une différence entre 2 $ et 2 cents ? »
V : « Oui, bien sûr. »
G : « Y a-t-il une différence entre 0.5 $ et 0.5 cents ? »
V : « 0.5 $ et 0.5 cent ? …………. »
G : « Y a-t-il une différence entre 1/2 $ et 1/2 cents ? »
V : « Oui »
G : « Y a-t-il une différence entre 0.002 $ et 0.002 cents ? »
V : « … »

En tout cas, c’est pas une bonne pub pour la société Verizon

Lien sur YouTube.

Voici un article du Figaro qui nous apprend que « le financement public civil de la recherche s’élève à 0,86 % du PIB ». On est loin des 3% attendus par l’Europe !
Votez recherche et enseignement supérieur !

No comment !

Launch of WIDER study on the World Distribution of Household Wealth

Résumé du rapport en Français.

Notion de jeux de rôles : si la date apparaît plusieurs fois dans une ligne de la table de faits, il faut créer des vues différentes de la table Date, en prenant soin de nommer différemment à la fois la table et les colonnes (par ex. « jour de commande » et « jour de livraison »…).

Concernant la dimension Produit qui est très courante, ses caractéristiques sont :

• un grand nombre de colonnes de texte descriptives.
• une ou plusieurs hiérarchies en plus d’un grand nombre d’attributs non hiérarchisés.

Cette dimension peut posséder plusieurs milliers de lignes et quelques précautions doivent être prises lors de la création de cette table à partir d’un fichier maître.

• Faire correspondre à la clé Produit opérationnelle une clé Produit artificielle.
• Insérer des séquences de texte lisibles remplaçant ou complétant les codes numériques du fichier maître Produit opérationnel.
• Contrôler tous les champs de texte pour éviter les erreurs d’orthographe, de valeurs impossibles ou des versions différentes du même attribut.
• Documenter les définitions, les interprétations et les sources des attributs des produits dans les métadonnées de l’entrepôt.

La dimension adresse de livraison.

Il est normal d’avoir plusieurs hiérarchies indépendantes dans cette table. Une hiérarchie naturelle est la hiérarchie géographique avec le pays, la région, le département, la ville, le lieu. Une autre hiérarchie possible est une hiérarchie par entreprise (une adresse de facturation peut regrouper plusieurs adresses de livraison). Les différentes hiérarchies peuvent avoir différents niveaux. Il peut arriver que la relation entre adresse de facturation et de livraison ne soit pas strictement hiérarchique (i.e. plusieurs factures pour une livraison). Dans ce cas, le grain de la table de dimension peut être affiné au niveau de la combinaison adresse de facturation/adresse de livraison, si cette relation non strictement hiérarchique reste exceptionnelle.

Sinon, il est préférable de définir une dimension supplémentaire « Adresse de facturation ». Il est inutile de créer une table portant les relations entre les deux dimensions, la table de faits porte déjà cette relation et répond efficacement à la question des corrélations entre dimensions.

La dimension dégénérée du numéro de commande n’est reliée à aucune table de dimension (c’est le propre d’une dimension dégénérée) car toutes les informations de la commande sont conservées dans les autres dimensions. Par contre, elle peut servir à regrouper les articles commandés ensembles. D’une façon générale, les dimensions dégénérées sont réservées à l’identification des transactions. Elles ne doivent surtout pas servir à stocker un code sans que sa réelle signification soit décrite dans une autre table.

La dimension fourre-tout (junk dimension) sert à stocker les différents indicateurs et drapeaux (flags) trouvés dans les données opérationnelles. Eventuellement, si le nombre de lignes est conséquent, on pourra créer plusieurs dimensions fourre-tout. Cette dimension soulage la table de faits et évite aussi la création d’un trop grand nombre de dimensions pour gérer ces indicateurs. On peut aussi créer une dimension fourre-tout pour stocker les commentaires trouvés dans les données.

Les devises multiples peuvent être gérées facilement à l’aide d’une table de conversion stockant les changes chaque jour et en ajoutant une dimension Monnaie (par pays).

Les faits de granularité différente ne doivent jamais être mélangés dans une même table de faits. Ou bien il faut répartir les faits de plus haut niveau au niveau le plus fin, ou bien il faut les mettre dans des tables de faits séparées. La première solution est la meilleure car elle permet la navigation entre les niveaux ; mais elle nécessite de définir les modalités d’allocation (activity based costing). Cette allocation sur le niveau de détail devrait être faite par une équipe dédiée plus fonctionnelle et non par les développeurs de l’entrepôt.

La facturation est le processus idéal pour commencer un entrepôt de données dans les sociétés qui expédient des produits ou vendent des services. Une table de faits de transactions de facturation est une des tables les plus puissantes de l’entreprise. Elle combine les clients, les produits et les composantes de la rentabilité.

Une table de faits des instantanés récapitulatifs voit ses lignes régulièrement mises à jour, contrairement aux autres tables de faits. Ce type de table de faits est mieux adapté aux processus de courte durée de vie ayant un identifiant du début à la fin.

Gestion des unités de mesure : s’il existe différentes unités de mesure comme par exemple le nombre de produits, le nombre de cartons, le nombre de palettes, etc. alors il est conseillé de stocker les différents facteurs de conversion dans la table de faits directement et non dans une dimension. La gestion des changements de facteur s’en trouve simplifiée.

Il me semble qu’il est aussi possible de stocker directement les quantités (dans les différentes unités de mesure) plutôt que les facteurs. Mais alors l’étude des changements de facteurs (qui représentent des changements de conteneurs) est plus difficile. Le facteur de conversion apparaît donc plus fondamental ici.

Comparaison des 3 types de table de faits.

Les tables de transactions seules ne peuvent pas offrir des modèles dimensionnels efficaces. Elles stockent toutes les transactions.

Les tables de faits instantanés périodiques résument les faits à la fin d’une période (la journée souvent). Elles facilitent le suivi de l’évolution de l’activité.

Les tables de faits instantanés récapitulatifs couvrent un laps de temps indéterminé, correspondant à la durée de vie de la transaction de produit. Cette table possède souvent une colonne « date de mise à jour de la ligne ».

Source : Ralph Kimball et Margy Ross, « Entrepôts de données, guide pratique de modélisation dimensionnelle« , 2ième édition.

Voici une initiative bien intéressante : Un Wiki pour établir une Constitution Citoyenne.

Sur le principe de l’encyclopédie libre Wikipedia, l’opportunité est offerte à tout un chacun de participer à la rédaction d’une constitution pour l’Europe. Peut-on faire plus démocratique ?
L’objectif général est clairement affiché :

Il est question ici d’écrire nous-même notre Constitution : une Constitution d’origine citoyenne, écrite par les citoyens pour les citoyens.

Cette initiative d’Etienne Chouard est issue du NON français au Traité de Constitution pour l’Europe.

Pour compléter ma note sur Un système de vote démocratique, voici une traduction et résumé de l’article paru dans la revue Physics World :

Depuis le « Non » des Pays-Bas et de la France au TCE, des physiciens et mathématiciens tentent d’appliquer leur savoir-faire en statistique pour proposer une solution au problème de distribution des votes entre les états membres du Conseil des Ministres, l’organe principal de prise de décisions de l’Union Européenne.

Le Conseil des Ministres est constitué de représentants politiques de chaque état membre qui votent au nom de leur pays respectif. Pour assurer que l’influence du vote de chaque pays reflète la taille de la population, sans pour autant « écraser » la voix des petits pays, les règles actuelles (celles du Traité de Nice de 2000) sont fondées sur un système compliqué appelé le « vote à la majorité qualifiée« . La voix de chaque représentant de pays est pondérée (avec un poids reflétant vaguement la taille de sa population) et pour qu’une proposition soit acceptée, il faut que 72% du poids total soit en sa faveur. De plus, il faut qu’au moins 13 pays sur les 25 états membres supportent la proposition et la population de ces 13 pays doit dépasser 62% de la population totale.

(Cela fait 3 points à vérifier pour qu’une proposition soit acceptée par le Conseil. Et il ne semble pas exister de justification raisonnable de ces règles).

Pour le TCE, les ministres ont voulu simplifier ce système en définissant la majorité qualifiée selon 2 règles :

1. Les états membres supportant une proposition doivent représenter plus de 60% de la population de l’Union Européenne.
2. et la majorité des états doivent la supporter (donc 13 états sur 25).

Bien que ce système soit simplifié et retire un peu de pouvoir aux pays à forte population par rapport au Traité de Nice, il a encore des défauts. Les gros pays (grande population) gardent un pouvoir de décision plus fort que les autres et les petits pays gagnent un pouvoir de décision disproportionné par rapport à leur taille. Ces effets combinés diminuent l’influence que peuvent avoir les pays moyens comme la Pologne ou l’Espagne.

Selon l’article des auteurs, il est possible de définir un système de vote sans ces défauts, dans lequel chaque citoyen de chaque état membre aurait le même pouvoir pour influencer les décisions prises en leur nom. Le système proposé est transparent, facile à mettre en oeuvre, efficace et gère sans problème l’ajout de nouveaux pays à l’Europe.

Les inconvénients inhérents au système de vote tel que celui de la Constitution Européenne sont connus depuis 1952 grâce au psychiatre et mathématicien Lionel Penrose (le père du physicien Roger et du mathématicien Olivier). Penrose a montré qu’un tel système favorisait les gros pays.

Penrose a envisagé un système plus juste fondée sur la loi de la racine carrée. Il a remarqué que lors des élections des représentants politiques dans un pays avec une population de taille N, un citoyen votant dans un gros pays a moins d’influence sur le résultat du vote qu’un citoyen votant dans un petit pays. Puisqu’un vote individuel particulier ne peut changer le résultat de l’élection que dans le cas d’un équilibre entre les différents représentants, le « pouvoir de vote » (ma traduction de « voting power« ) d’un citoyen doit être proportionnel à la probabilité qu’une telle configuration (d’égalité entre les parties) se produise. 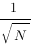En prenant pour hypothèse que les votes ne sont pas corrélés, Penrose a calculé que cette probabilité est proportionnelle à , l’inverse de la racine carrée de N (la taille de la population).
Dans le cas de l’Europe, le gouvernement élu nomme ensuite un ministre pour voter au nom du pays dans le Conseil des Ministres, où le système de vote devrait idéalement représenter les vues de chaque citoyen européen de façon égalitaire quelque soit sa nationalité. Il s’ensuit que le poids du vote de chaque pays devrait être proportionnel à la racine carrée de sa population, afin de compenser le facteur inverse de la racine carrée de N.

La loi de la racine carrée de Penrose a été proposée comme base d’un système de vote pour le Conseil des Ministres en 1998 par Annick Laruelle de l’Université Catholique de Louvain en Belgique et Mika Widgren de la « Turku School of Economics and Business Administration » de Finlande.

Cependant, cette loi de Penrose affectant un poids au vote d’un pays n’est pas suffisante, car elle ne garantit pas que le pays peut exercer son pouvoir dans la prise de décisions. Un contre-exemple simple est donné avec deux pays ayant respectivement un vote pesant 51% et 49%, et un système qui adopte toute proposition s’il y a une simple majorité de votes (majorité qualifiée à 50%). Le pays ayant une voix pesant 51% gagnerait à chaque fois. Il aurait un pouvoir de vote de 100%. Il est donc nécessaire de distinguer entre pouvoir de vote et poids d’un vote. Un tel cas s’est produit (pendant 15 ans !) dans l’ancienne CEE : le Luxembourg avait un vote qui semblait représenter un poids plus lourd que ne le méritait sa petite population, mais malgré cela, son vote n’avait strictement aucune influence sur les décisions prises. Son pouvoir de vote était de 0. Autrement dit, aucune alliance de pays n’avait besoin du vote du Luxembourg pour faire pencher la balance de son côté.

Pour généraliser, un pays a du pouvoir de vote lorsque son vote peut être décisif en cas de ballottage. Ce concept peut être formalisé en considérant toutes les coalitions possibles dans lesquelles un pays peut prendre part. Le pouvoir de vote est défini numériquement comme la proportion de coalitions dans lesquelles le vote d’un pays est décisif. Cette proportion a été trouvée indépendamment par Penrose en 1946 et par l’américain John Banzhaf en 1965, et est connue sous le nom d’index de Banzhaf.

Les 25 états de l’Union Européenne peuvent former plus de 33.5 millions de coalitions (ce sera 4 fois plus avec la Roumanie et la Bulgarie). Pour un choix de poids et une règle de majorité qualifiée donnés, il est possible de calculer les cas où un pays a un vote décisif pour chacune de ces coalitions. En d’autres mots, le pouvoir de vote d’un état, mesuré par l’index de Banzhaf, peut être calculé.

Le compromis jagiellonien.

Sachant calculé le pouvoir de vote de chaque état pour chaque système de vote, les auteurs ont cherché un système qui distribue ce pouvoir selon la loi de Penrose.

En 2004, un des auteurs a proposé un système fondé sur un seul critère : le poids d’un vote d’un état membre doit être proportionnel à la racine carrée de sa population et la décision est prise si la somme des poids des pays votant en sa faveur dépasse 62% du poids total. Ce système est très simple, mais les auteurs se sont posé la question de savoir d’où venait ce seuil de 62%. Ils ont calculé la façon dont varie le pouvoir de vote (l’index de Banzhaf) en fonction de ce seuil et ont observé un « point critique » : lorsque la majorité qualifiée s’approche de la valeur de 62%, le pouvoir de vote de chaque pays devient égal au poids du vote indépendament de la taille de sa population. A ce seuil, le pouvoir de vote est donc égal à la racine carré de la population.

La loi de Penrose est donc respectée et chaque citoyen a le même pouvoir de vote, avec un système de vote plus simple que celui du TCE ou du Traité de Nice. Par ailleurs, tout élargissement de l’Europe conduit à recalculer le seuil de la règle de la majorité qualifiée. Par exemple, il serait de 61.4% pour une Europe à 27.

Le système proposé par ces auteurs a fortement intéressé les experts de la théorie des votes et a été appelé « compromis jagiellionien » par les media. Avant le sommet européen à Bruxelle en juin 2004, une lettre ouverte en faveur de ce système de vote pour le Conseil des Ministres soutenue par plus de 40 scientifiques dans 10 pays européens a été envoyée aux institutions européennes et aux gouvernements des états membres.

La réaction des politiques a été diverse, mais a plus dépendu de la façon dont le pays concerné été affecté par le partage des votes que des critères universels tels que la simplicité et l’objectivité. Quand un système semblable a été mis en avant par les diplomates suédois en 2000, le premier ministre suédois Göran Persson a dit « Notre formule a l’avantage d’être facilement comprise par l’opinion publique et pratique à utiliser dans une Europe élargie… C’est transparent, logique et loyal. Peut-être que c’est pour cela que ça ne plaît pas à tout le monde. » Le précédent premier ministre irlandais John Burton a aussi fait un grand nombre de louanges aux système de vote fondés sur la loi de Penrose et le compromis jagiellonien a été soutenu par plusieurs politiques en Pologne et a été étudié par des chercheurs du gouvernement anglais en 2004.

Le compromis jagiellonien offre aux futurs négociateurs un système simple, mais objectif fondé sur des principes rationnels qui garantissent un même pouvoir pour tous les citoyens d’Europe.