Que faire en cette journée spéciale ?

Si vous aimez la musique, ce site vous propose de créer votre propre musique basée sur les décimales de

Pour les amateurs de films, l’excellent film d’Aronofsky: Pi.

Question intéressante : que met-on entre parenthèses ?
La réponse chez Tom Roud : Arithmétique algorithmique.

Ma fille en CM1 a trouvé la bonne réponse alors que ma fille en CE2 utilise plutôt le raisonnement algorithmique…

Source : The Importance of the Equal Sign.

Du 7 juin au 25 juillet 2010, la Société Européenne pour les Mathématiques et les Arts propose une exposition à l’IHP.

En cherchant d’autres liens en rapport avec le chaos et l’art mathématique, j’ai découvert ce site récent qui montre des sculptures du chaos.

A voir également de magnifiques images d’une « mandelbox« .

En papillonant un peu plus sur Internet, je suis aussi tombé sur ces applications :

• pour ajouter un effet Droste à vos photos : SeamlessMaker
• pour faire des noeuds : KnotsBag.

Appréciez… et amusez-vous…

Je viens de passer quelques temps à lire ce blog : Inclassables Mathématiques Le blog 2.0

J’y ai trouvé quelques liens intéressants.

En voici 2 pour pratiquer les maths sur le web :

1. Le premier permet de créer des figures en ligne et d’y insérer des équations mathématiques.
2. Le second permet de causer mathématique en ligne, autrement dit de placer des équations dans une conversation en ligne. Essayez donc de faire la même chose avec MSN…

Et là, vous pouvez rechercher votre date de naissance (ou toute autre séquence de chiffres) dans les décimales de . Ma date de naissance n’y est pas si on l’écrit selon le format français (jjmmaaaa). Par contre, je la trouve en l’écrivant selon le format anglais (mmjjaaaa) ou le format iso (aaaammjj).

Pour comprendre un peu mieux les probabilités de trouver une séquence dans , voyez ici.

Source : Les articles d’Inclassables mathématiques là, là et là.

Voici un article de revue qui peut intéresser les joueurs Les auteurs étudient de façon précise la dynamique du  jet d’une pièce de monnaie d’épaisseur non nulle.

Ils étudient la configuration finale de la pièce (pile, face, tranche) en fonction des paramètres initiaux que sont la position, la configuration, l’impulsion et le moment angulaire à l’origine du mouvement. Chaque point de l’espace des paramètres initiaux conduit à une configuration finale. La configuration finale a 3 bassins d’attraction dans l’espace des paramètres : le bassin d’attraction « pile », le bassin d’attraction « face » et le bassin d’attraction « tranche » (c’est-à-dire les paramètres initiaux conduisant à « pile », « face » ou « tranche »).

Les équations gouvernant le mouvement de pièce sont celles de la mécanique de Newton. Ces équations sont déterministes et donc à moins d’une influence externe aléatoire ou d’une dynamique chaotique, le résultat du jet est déterminé uniquement par les conditions initiales.

Les auteurs affirment que la configuration finale de la pièce peut être prédit de façon précise lorsque les conditions initiales sont connues. Il n’y a pas d’incertitude dynamique due à une divergence exponentielle due à une sensibilité aux conditions initiales ou à des frontières fractales des bassins d’attraction.

L’analyse a été faite avec une pièce en 3 dimensions ayant une épaisseur. Le cas des pièces uniformes et non-uniformes, l’influence de la résistance de l’air et l’impact de la pièce sur le sol ont également été étudiés.

Il en résulte que

1. La résistance de l’air dévie la trajectoire du centre de masse de la pièce de la verticale et amortit les rotations. Elle peut être négligée lorsque la hauteur est faible.
2. Les rebonds de la pièce sur la surface influent sur le résultat : des rebonds successifs introduisent une sensibilité accrue aux conditions initiales indiquant la mise en place d’un phénomène chaotique.

Les frontières entre les différents bassins d’attraction dans l’espace des paramètres initiaux sont lisses (non fractales). On trouve donc des régions dans l’espace des paramètres pour lesquelles on peut déterminer de façon certaine le résultat du lancer. Cependant, en pratique, ces régions sont si petites qu’un changement des paramètres initiaux permet facilement de franchir la frontière entre deux régions.

On peut donc continuer à tirer à pile ou face lorsque l’on veut prendre une décision de manière aléatoire, du moment que l’on ne maîtrise pas complètement les paramètres initiaux ou que la pièce rebondit plusieurs fois…

Référence : Physics Reports : Dynamics of coin tossing is predictable de J. Strzałko et al.

Voici un livre sur les mathématiques utilisées en physique quantique : Guide to Mathematical Concepts of Quantum Theory. Il est conçu comme un guide présentant les différents concepts mathématiques nécessaires pour aborder la théorie quantique.

Une expérience de physique quantique peut se découper en plusieurs phases :

1. la phase de préparation
2. la phase d’évolution
3. la phase de mesure

Selon les descriptions, la phase d’évolution peut être absorbée dans l’une des deux phases (voir par exemple p. 32 de mon résumé du livre de Bitbol).

On retrouve ces étapes dans les différents chapitres du livre :
Les auteurs introduisent étape par étape les concepts de la théorie quantique d’un point de vue mathématique. Le livre commence par un rappel sur l’espace de Hilbert, puis enchaîne sur les définitions des états quantiques et de leurs effets (définis comme les valeurs possibles que peuvent prendre les états quantiques lors des mesures). Les observables sont vues comme une collection d’effets et un chapitre entier leur est dédié. La phase d’évolution est présentée au chapitre 5 avec les opérations et les canaux quantiques. Puis viennent la mesure et l’intrication.

Les auteurs ne font pas que présenter le formalisme mathématique de la physique quantique, ils abordent également des problèmes d’actualité tels que la cryptographie quantique avec la distribution des clés quantiques, les ordinateurs quantiques (théorème de non clonage quantique)…

L’intérêt du livre est double : il se propose d’être un guide mathématique des concepts de la théorie quantique et ce guide est objectif en ce sens qu’il ne propose aucune interprétation du formalisme quantique (voir la fin de ce billet pour un mot sur les interprétations ou bien l’article de wikipedia plus complet). C’est ce qui le rend intéressant. Même si notre esprit éprouve des difficultés à appréhender le monde quantique, il est tout de même capable de produire une théorie mathématique falsifiable.

Comprendre les mathématiques capables de reproduire les divers phénomènes de la nature me paraît un bon point de départ pour comprendre la nature elle-même.

Une émission à écouter sur France Culture.

Quand ?
Vendredi à 14h.

Ce livre de 300 pages pose la question du constructivisme mathématique en tant que formalisme pour la physique quantique des particules : Constructive physics.

En mathématique constructive, tout objet doit pouvoir être construit : un objet est défini par un algorithme qui permet de le construire effectivement. Un objet non défini par un algorithme n’existe pas.
La logique constructiviste n’impose pas le principe du tiers exclu comme la logique classique.

Sur ce aspect, elle se rapproche donc déjà de la logique de la mécanique quantique et l’auteur n’est pas le premier à s’intéresser aux liens potentiels entre ces deux logiques (voir cet article).

Je n’ai pas lu le livre cité ci-dessus, mais le sujet m’intéressant, j’essaierai de trouver le temps de le faire et éventuellement d’en rapporter ici ce que j’aurai pu comprendre.

Voici un énoncé de jeu de hasard pas très conventionnel.

Le jeu se joue avec un dé normal à 6 faces numérotées de 1 à 6. Le dé n’est pas pipé. La probabilité de tirer une des six faces est donc de 1/6. Un joueur annonce :

« si le jet du dé sort un nombre pair alors ce sera le nombre 2 ou bien si le jet sort un nombre inférieur à 5 alors ce nombre sera inférieur à 4. »

Il faut comprendre « inférieur » au sens « inférieur strict ».
La question est la suivante :
Quelles sont les chances de gagner de ce joueur ?

S’il y a des amateurs de jeux de hasard ou des mathématiciens parmi mes lecteurs, je serais curieux de connaître leur estimation ; et évidemment, pour ceux qui auraient la bonne réponse, le raisonnement pour y arriver. D’après l’article duquel je tire cet énoncé, la théorie des probabilités usuelle n’est pas capable de répondre à ce type de questions. Je ne donne pas la référence immédiatement. J’attends qu’il y ait quelques réponses d’abord (et s’il n’y a pas de réponse, c’est que ça n’intéresse personne et ce ne sera pas la peine de donner la référence ).
Avis aux amateurs…

John Baez a écrit un billet sur le nombre 24. Ce nombre correspondant au jour de mon anniversaire (dans le calendrier Grégorien), je suis obligé de laisser un lien sur cet article dans lequel on apprend beaucoup de choses :
More Mysteries of the Number 24 | The n-Category Café

Quelques liens en rapport avec 24 :

• le réseau de Leech
• La conjecture « Monstrous Moonshine »
• Les 24 éléments du groupe tétrahédral binaire
• L’icositetrachoron ou 24-cell
• 24 est le seul nombre entier non trivial tel que la somme des carrés jusqu’à ce nombre soit un carré :

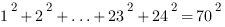
Quelqu’un connaitrait-il une démonstration visuelle de cette relation sur les carrés ?