« Nine formulations of quantum mechanics » de D. F. Styer et al. dans American Journal of Physics — March 2002 — Volume 70, Issue 3, pp. 288-297.Voici un article qui présente brièvement et pédagogiquement 9 formulations de la mécanique quantique (et non ses interprétations, la nuance étant que les formulations sont différentes approches mathématiques alors que les interprétations sont plus du point de vue conceptuel). On pourra trouver l’article ici (si le lien est toujours valide).

Je note ici les points essentiels de chaque formulation. Cependant, l’article donne en plus les références incontournables et également les références historiques. Pour chaque formulation, les auteurs s’attachent également à considérer comment se différencient les bosons des fermions, ce dont je ne parlerai pas dans ce post.

1. La formulation matricielle de Heisenberg. C’est la formulation dans laquelle les observables sont représentées par des matrices (aussi appelées « opérateurs »). Les valeurs propres des matrices correspondent aux valeurs mesurables dans les expériences. Les états quantiques sont des vecteurs indépendant du temps. La dépendance temporelle est portée par les opérateurs. Cette formulation est très pratique pour résoudre les problèmes d’oscillateurs harmoniques et de moments angulaires.
2. La formulation de la fonction d’onde de Schrödinger. Le concept important n’est plus la quantité mesurable, mais l’état quantique qui est une fonction complexe dans un espace de configuration à 3 dimensions (pour 1 particule). Contrairement à ce que souhaitait Schrödinger, la fonction d’onde n’a pas d’existence réelle ; elle est principalement un outil de calcul des probabilités des observations possibles. La dépendance temporelle est portée par la fonction d’onde, et non plus par les opérateurs. C’est la formulation la plus courante de la mécanique quantique.
3. La formulation de l’intégrale de chemin de Feynman. Le concept important n’est plus l’état mais la probabilité de transition entre un état initial et un état final. Dans cette formulation, on énumère tous les chemins possibles permettant de passer de l’état initial à l’état final. A chaque chemin est affectée une « amplitude » de probabilité. Le module carré de la somme sur tous les chemins de ces amplitudes donnent la probabilté de transition recherchée. Cette formulation est loin d’être pratique à utiliser sauf dans les simulations de Monté-Carlo de systèmes quantiques.
4. La formulation de la distribution de (quasi-)probabilité dans l’espace des phases de Wigner. Le concept central est la distribution de l’espace des phases notée 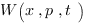qui remplace la fonction d’onde. Cette distribution offre l’avantage d’être purement réelle (contrairement à la fonction d’onde qui est complexe) et de donner facilement la densité de probabilité de la position ou de l’impulsion par simple intégration. Mais ce n’est pas une densité de probabilité dans l’espace des phases car elle peut prendre des valeurs négatives. Elle n’est pas non plus la façon la plus économique d’enregistrer de l’information sur l’état quantique. Son utilisation est essentiellement en optique quantique. Elle est très utile pour considérer la limite classique.
5. La formulation de la matrice densité (ou opérateur densité). Cette formulation est particulièrement performante lorsqu’il s’agit de travailler avec des états mixtes (faisant intervenir des mélanges statistiques d’états quantiques). La fonction d’onde ne permet de représenter simplement des mélanges statistiques d’états. La matrice densité est toujours hermitienne. Les calculs de moyenne d’opérateurs se font à l’aide de la formule de trace. Comme la distribution de Wigner, la matrice densité est coûteuse en termes de stockage d’information sur l’état quantique. Néanmoins, elle trouve des applications dans plusieurs domaines de la physique et en particulier en physique quantique statistique.
6. La formulation de la seconde quantification (ou formalisme du nombre d’occupation). Dans cette formulation en étroite relation avec la théorie quantique des champs, le concept central est celui d’opérateur de création et d’annihilation de particule. Cette formulation est fondamentale pour l’étude des systèmes à plusieurs particules. Les opérateurs agissent sur un état de vide quantique de particule et permettent la création de particules à partir du vide ou la destruction de particules existantes.
7. La formulation variationnelle. Elle s’inspire du principe de Hamilton (principe de moindre action) de la physique classique. Le concept ici est la fonction d’onde qui minimise l’intégrale d’action sur le temps et l’espace de configuration. Ce critère de minimisation est équivalent à l’équation de Schrödinger. Cette formulation est un outil puissant pour étendre la physique à de nouveaux domaines.
8. La formulation de l’onde pilote de de Broglie-Bohm. Cette formulation propose une description corspuculaire des particules dans l’espace physique et en même temps utilise une fonction d’onde (l’onde pilote) dans l’espace des configurations qui contraint le mouvement des particules. Les équations du mouvement font apparaître une énergie potentielle d’origine purement quantique : le potentiel quantique. Ce potentiel est le responsable des phénomènes quantiques. Cette formulation n’est pas simple d’utilisation mais elle offre une vision proche de la physique classique.
9. La formulation de Hamiton-Jacobi. Dans cette formulation, un changement adéquat de variable permet d’écrire les équations du mouvement avec l’ensemble de variables dites d’action et d’angle. La formulation de la mécanique quantique sous cette forme est récente (1983) et est due à R. Leacock et M. Pagdett. Le concept central est la fonction principale de Hamilton . Cette approche permet d’obtenir des valeurs propres de l’énergie sans recourir aux vecteurs propres, très utile dans les problèmes d’états liés.

Ces différentes approches formulent de manière différente l’étrangeté de la mécanique quantique, mais aucune ne peut l’éliminer.

Un mot sur les interprétations :

• Il y a l’interprétation des mondes multiples d’Everett dans laquelle toutes les histoires existent en parallèle, mais seule une histoire nous concerne. C’est probablement l’interprétation la plus naturelle lorsque l’on part de la formulation de Schrödinger. Ce qui ne veut pas dire selon moi que c’est l’interprétation qui a le plus de sens.
• Il y a aussi l’interprétation transactionnelle de Cramer dans laquelle à la fois sources et détecteurs de particules émettent une onde (retardées et avancées). Les interférences destructives assurent que la particule arrive sur le détecteur après avoir quitté la source. Cette interprétation que je connais très peu permettrait de mieux visualiser des processus quantiques complexes et d’analyser rapidement des situations autrement paradoxales.
• La théorie de la fonctionnelle densité de Hohenberg et Kohn est un outil très puissant pour traiter les états fondamentaux de systèmes complexes en matière condensée et en chimie.
• La théorie de la décohérence s’attache à expliquer pourquoi le monde macroscopique n’est pas quantique.
• Les histoires consistentes de Griffiths sont une autre interprétation.
• La localisation spontannée continue étudie l’effondrement de la fonction d’onde en modifiant l’équation de Schrödinger.

A découvrir :

The Music of the Quantum

Une composition de Jaz Coleman jouée en mars 2003 à New York.

La musique idéale pour lire de la physique quantique

Sur le site, vous pouvez écouter le concert et même visionner des vidéos : sélectionnez le lien « The music of the quantum ».