Mécanique quantique : Mythes et faits

Dans cet article, Nikolic passe en revue les assertions les plus courantes au sujet de la mécanique quantique qui n’ont pas de justification solide :
[quant-ph/0609163] Quantum mechanics: Myths and facts

L’article est très pédagogique et donne une centaine de références pour approfondir les différents sujets abordés.

Sans rentrer dans le détail, je résume les mythes « révélés » dans ce papier ci-dessous :

• La dualité onde-corpuscule. Il n’y a pas en fait de dualité onde-corpuscule. La mécanique quantique a des aspects ondulatoires la plupart du temps et corpusculaires dans certains cas, sans pour autant être complètement décrite ni par l’une ni par l’autre des théories classiques. Pour Nikolic, la physique classique n’est qu’une approximation de la mécanique quantique (ce qui à mon avis est aussi un mythe). Et l’interprétation bohmienne de la mécanique quantique est la seule à offrir une sorte de vraie dualité onde-corpuscule.
• La relation d’incertitude temps-énergie. En mécanique quantique, les relations d’incertitude se déduisent des relations de commutation des opérateurs. Le temps, lui, n’est pas un opérateur comme c’est le cas pour la position et l’impulsion par exemple. Et le théorème de Pauli, en interdisant le remplacement du temps par un opérateur, rend impossible la construction d’une relation d’incertitude temps-énergie. Busch a tenté de modifier des axiomes de la théorie quantique pour pouvoir introduire une relation de commutation entre un opérateur temps et le hamiltonien (opérateur énergie). Cependant, il semble qu’il y ait un contre-exemple (théorique) à la relation d’incertitude temps-énergie (article de Aharonov-Bohm de 1961).
• La mécanique quantique implique une nature fondamentalement aléatoire. Cette assertion est liée au problème des théories à variables cachées. Même le théorème de Bell qui exclue une partie des théories à variables cachées, n’exclue pas qu’il puisse exister des théories à variables cachées déterministes capables de rendre compte des phénomènes quantiques. C’est d’ailleurs le cas avec la théorie de Bohm.
• Il n’y a pas de réalité en dehors de la réalité mesurée. Les variables classiques discrètes peuvent être représentées par un formalisme probabiliste équivalent au formalisme quantique à l’aide des nombres complexes, de vecteurs et de matrices. Cependant, dans cette reformulation de la physique classique, les matrices ne représentent pas des quantités physiques, mais des opérateurs décrivant des transformations. Au contraire, pour la physique quantique, les matrices ont un double rôle d’opérateurs et de variables physiques. Du fait de la non commutativité entre certains opérateurs, la mesure simultanée de variables physiques (opérateurs) est soumise à conditions. En particulier, les mesures dépendent du contexte expérimental. Et des théorèmes comme les inégalités de Bell montrent qu’il n’y a pas de théorie non contextuelle ou non locale qui puisse rendre compte des expériences EPR. Le raisonnement classique qui attribue des valeurs bien déterminées aux variables physiques indépendamment du contexte n’est pas applicable en mécanique quantique. Le résultat de Hardy le montre d’une manière très simple avec 2 particules intriquées (voir les équs 43 à 46). Les solutions envisagées par les physiciens pour résoudre ce paradoxe sont diverses, mais aucune n’est encore vraiment complètement satisfaisante. Parmi elles, il y a :
• la logique quantique, mais la déviation par rapport à la logique classique est considérée trop importante,
• la notion de variable préférée : toutes les observables n’ont pas nécessairement de réalité physique. Certaines variables seulement doivent être considérées comme étant réelles. Cette solution peut être valable dans certains cas (par ex. la position peut être considérée plus physique que l’impulsion qui est souvent déduite de mesures de positions), mais elle n’est certainement pas valable pour toutes les situations rencontrées en mécanique quantique.
• la contextualité : là, il y a deux comportements distincts. Le premier est l’interprétation orthodoxe dans sa déclinaison dure, qui prétend qu’il n’y a pas de sens à donner des valeurs à des quantités non mesurées. Dans sa déclinaison moins radicale, l’interprétation orthodoxe laisse une porte ouverte à l’existence de valeurs pour des variables non mesurées, mais s’interdit d’en parler. Le deuxième comportement est l’approche suggérée par les théories à variables cachées, à savoir que la mécanique quantique ne donne pas une description complète de la réalité. Les théorèmes à la Bell n’interdisent pas en effet toutes les théories à variables cachées, mais seulement les théories locales naïves. L’interprétation orthodoxe dure se décline encore en plusieurs branches :
• le concept d’information sur la réalité serait plus important que celui même de réalité
• la réalité est relative ou relationnelle
• des corrélations entre variables existent même si les variables elles-mêmes n’existent pas.
• Concernant les théories à variables cachées, l’interprétation proposée par Bohm combine la possibilité d’existence de variables préférées (la position) et l’existence de variables cachées (la position même lorsqu’elle n’est pas mesurée). Nikolic semble montrer ici un penchant pour cette théorie.
• La mécanique quantique est locale/non locale. Il est communément admis que la mécanique classique est locale. Par contre, le cas de la mécanique quantique est moins clair. Un principe de localité est souvent utilisé pour réfuter les théories à variables cachées. Tout d’abord, ce principe n’est qu’une hypothèse. Ensuite, contrairement à ce que prétendent certains, la non-localité ne contredit pas nécessairement la théorie de la relativité. Enfin pour Nikolic, la communication instantanée (plus vite que la vitesse de la lumière) n’est pas exclue par la théorie de la relativité comme le montre la théorie des tachyons (particules encore hypothétiques ayant une vitesse supraluminique). Selon certains physiciens, la communication supraluminique ne contredit pas le principe de causalité. Cela aussi serait donc un mythe. Les expériences de type EPR font pencher la balance vers une mécanique quantique non locale (les corrélations entre sous-systèmes sont non locales). Il existe cependant des physiciens qui vont jusqu’à nier l’existence d’une réalité pour maintenir le principe de localité.
• Il existe une mécanique quantique relativiste bien définie. L’équation de Klein-Gordon (généralisation relativiste la plus simple de l’équation de Schrödinger) pose de gros problèmes d’interprétation. En particulier, le module carré de la fonction d’onde qui était interprétée comme une probabilité en mécanique quantique non relativiste ne peut plus l’être dans ce formalisme. Et ce même en restreignant les solutions à des valeurs positives de la fréquence. L’équation de Dirac n’a pas de problème d’interprétation en terme de probabilités, mais elle est limitée à la description des particules de spin 1/2, l’équation de Klein-gordon décrivant les particules de spin 0 et les équations de Maxwell celles de spin 1. Les équations de Maxwell ont aussi un problème d’interprétation du même type que les équations de Klein-Gordon.
• La théorie quantique des champs résoud le problème de la mécanique quantique relativiste. La méthode de la seconde quantification donne le statut d’opérateur à la fonction d’onde. Les coefficients 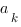du développement de Fourier de la fonction d’onde sont des opérateurs et leurs relations de commutation sont postulées. En théorie quantique des champs, le concept essentiel n’est plus la fonction d’onde mais l’opérateur de champs défini à partir de l’opérateur fonction d’onde et son hermitique conjugué Equ. (76). Là encore, les relations de commutation de ces opérateurs sont postulées (mais de celles-ci on peut maintenant déduire celles sur les 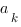). La théorie quantique des champs semble donc ne faire que repousser le problème plus loin, sans le résoudre vraiment.
• La théorie quantique des champs est une théorie des particules. La théorie quantique des champs ne tranche pas sur la question de savoir si le monde est formé de particules ou de champs. Il se pourrait même que ce soit ni l’une ni l’autre solution, mais des cordes (theorie des cordes).
• L’entropie d’un trou noir est proportionnelle à sa surface. En physique classique, l’entropie en tant que quantité extensive est proportionnelle au volume plutôt qu’à la surface. En théorie classique de la gravité, les 4 lois de la thermodynamique classique ont leur équivalent pour les trous noirs. Cependant, ces lois pour les trous noirs ne sont que des analogies et n’ont pas encore de dérivation à partir d’une formulation microscopique. C’est ce que cherchent les différentes approches de gravité quantique.