Les aspects positifs du principe d’incertitude de Heisenberg

P. Busch, T. Heinonen et P. Lahti proposent un article de revue sur le principe d’incertitude de Heisenberg.

Pour rappels, le principe d’incertitude s’énonce en général de l’une des manières suivantes :

1. Il n’est pas possible de préparer un état quantique pour qui aura à la fois une position et une impulsion précises,
2. Il n’est pas possible d’obtenir la position et l’impulsion d’une particule par des mesures effectuées à la suite l’une de l’autre.
3. La position et l’impulsion ne peuvent pas être mesurées en même temps.

Ces énoncés évoquent tous une limitation de la physique quantique par rapport à la physique classique pour laquelle il est possible de faire des mesures aussi précises que l’on veut de la position et de l’impulsion des particules. Toutes les formulations du principe d’incertitude impliquent qu’il n’existe pas de mesure sans perturbation.
Plutôt que de voir ce principe comme une limitation, les auteurs formulent 3 énoncés qui le présentent de façon positive :

1. Il est possible de préparer des états quantiques pour lesquels la position et l’impulsion prennent des valeurs « imprécises » (unsharp) avec des degrés d’imprécision satisfaisant une relation exprimant un compromis,
2. La perturbation mutuelle des mesures de position et d’impulsion effectuées à la suite l’une de l’autre, peut être contrôlée à l’aide d’une relation appropriée de compromis entre la précision d’une mesure et la perturbation de l’autre,
3. Il est possible d’obtenir des mesures conjointes approximatives de la position et de l’impulsion avec des précisions satisfaisant une relation appropriée de compromis.

Plusieurs théorèmes sont ensuite démontrés. En particulier, concernant le point 1, il est montré que

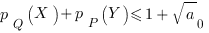
si 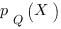(resp. 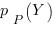) est la probabilité que la position (resp. l’impulsion) soit dans l’intervalle 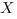(resp. 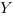). On a 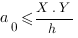, 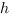étant la constante de Planck et 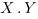étant la taille de la cellule dans l’espace des phases dans laquelle se trouve la particule. Ce théorème est une conséquence des résultats classiques des transformations de Fourier.
Au lieu de se contenter de cette formule, on peut aussi poser la question réciproque de calculer la plus petite cellule de l’espace des phases que l’on peut trouver si l’on se donne des niveaux de probabilité de trouver la position et l’impulsion dans les intervalles 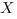et 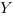respectivement.

Concernant le point 2, Werner a exprimé le degré de perturbation lors de mesures séquentielles, d’une façon complètement générale en faisant intervenir la distance entre 2 observables définies sur l’espace des phases. Le théorème de Werner pose que pour 2 observables marginales 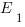et 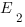d’une observable 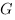sur l’espace des phases,

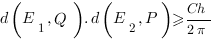vaut environ 0.3047.

Dans le paragraphe 3.4, les auteurs remarquent que la quantification de l’erreur et de la perturbation engendrées par la mesure est traditionnellement modélisée d’après un raisonnement classique. Et bien que Appleby et Ozawa aient introduit des relations d’incertitude en termes de mesures d’erreur classique, la signification opérationnelle de ces relations n’est pas claire. L’erreur et la perturbation classique contiennent toutes deux un terme de bruit — équ. (38), bien défini, mais elles contiennent également un terme qui n’a pas de sens bien défini opérationnellement — équ. (39). Ce dernier terme fait intervenir l’espérance du carré de la différence entre 2 opérateurs qui peuvent ne pas commuter.

Enfin, pour le point 3, bien que les opérateurs de position et d’impulsion ne commutent pas, des fonctions de la position et de l’impulsion peuvent commuter sous certaines conditions de périodicité (Théorème 5). Ces fonctions permettent de modéliser des situations en physique du solide où un électron dans un cristal peut être arbitrairement proche des atomes et avoir en même temps une impulsion précise.

Mais le point 3 peut aussi être valable dans des situations plus générales. C’est ce que montre le théorème 7 qui dit qu’une position approximative et une impulsion approximative peuvent être mesurées conjointement si et seulement si elles ont une observable covariante de l’espace des phases.

Les expériences.

Le dernier paragraphe se penche sur les expériences et tests du principe d’incertitude.

Il apparaît que les expériences sont peu nombreuses, même encore aujourd’hui. Les quelques expériences rapportant une confirmation du principe d’incertitude en rapport avec le point 1 sont des expériences de diffraction et d’interférences avec des neutrons ou d’autres particules comme dans l’expérience de l’équipe de Zeilinger avec des molécules de fullerène. Mais ces expériences ne constituent pas des tests directs du principe d’incertitude concernant la position et de l’impulsion. Elles utilisent une description approximative de la fonction d’onde à l’infini (équivalente à la diffraction de Fraunhofer en optique classique). Ainsi, ce qui est testé est une relation d’incertitude découlant du lien par la transformation de Fourier de la position et de l’impulsion et de l’équation d’évolution de Schrödinger libre.

Concernant le point 2, les expériences étudiant la relation imprécision et perturbation de la mesure sont les moins développées. Mais cela s’explique par le fait que les théories vraiment opérationnelles sont encore récentes.

Pour le point 3, il ne semble pas y avoir d’expérience réalisant une mesure conjointe de la position et de l’impulsion. Il existe par contre des expériences d’optique réalisant des mesures conjointes d’observables incompatibles autres que la position et l’impulsion.

Les opposants au principe d’incertitude

En 1970, Ballentine était arrivé à la conclusion qu’une description des mesures conjointes de la position et de l’impulsion en termes de probabilités jointes ne pouvait se faire qu’en étendant la théorie existante. C’est ce qu’ont fait les auteurs de l’article avec l’introduction des opérateurs de mesure positifs et des observables de l’espace des phases.

Une autre catégorie d’opposants prétend que les mesures conjointes sont possibles avec une précision aussi grande que l’on veut. Parmi eux, il y a Popper et Margenau. En 1934, Popper avait conçu une procédure de mesure conjointe sur des paires de particules intrinquées (entangled). Mais von Weizsäcker a rapidement montré l’erreur faite par Popper qui l’a reconnue ensuite. Pour Popper, sa proposition aurait pu ensuite inspirer le fameux article EPR.

Dans les expériences proposées par les opposants, la mesure de l’impulsion est faite en général à partir de la détermination de deux positions. Mais ce type de mesure est dictée seulement par le raisonnement classique et n’a pas de signification opérationnelle.

Plus tard, Popper a proposé une autre expérience de pensée pour mettre en défaut le principe d’incertitude. Kim et Shih ont implémenté la réalisation expérimentale et ont obtenu des résultats controversés. Au final, il semblerait que le principe d’incertitude n’est pas violé (Voir Qureshi entre autres).