Le prochain Séminaire Poincaré aura lieu le 8 décembre. Le sujet est le « spin« .

Mise à jour :
Programme provisoire

Matinée
10 h 30 Jürg Fröhlich: Introduction au spin
11h 30 Autour d’Albert Fert, prix Nobel 2007

Après-midi
14h Gerald Gabrielse: Mesure du spin
15h15 Frank Wilczek: Spin et physique théorique
16h30 Pierre-Jean Nacher: Applications médicales

Le programme est ici au format pdf.

Quantiki est un Wiki sur l’information quantique. On y trouvera des informations, des événements, quelques tutoriaux, une encyclopédie sur l’information quantique, une liste de problèmes en cours et plein d’autres liens.

Bref beaucoup de ressources pour tous ceux qui s’intéressent à l’information quantique.

En informatique, les nombres aléatoires sont plutôt difficiles à obtenir. En fait, il est impossible de créer de vrais nombres aléatoires à partir d’algorithmes fonctionnant sur les ordinateurs classiques. Les algorithmes permettant de générer des nombres dits pseudo-aléatoires sont obligés de se répéter au bout d’un certain temps.
Les nombres aléatoires sont très importants pour divers algorithmes d’optimisation (Monte-Carlo, algorithmes évolutionnaires…), de simulation statistique, cryptographie… Et lorsqu’ils ne sont pas vraiment aléatoires, les résultats peuvent être faussés.
Jusqu’à récemment, il fallait se contenter de générateurs de nombres pseudo-aléatoires. Un des meilleurs algorithmes pour la génération de nombres pseudo-aléatoires est le Mersenne Twister. Cet algorithme n’est par contre pas adapté pour les besoins de la cryptographie.

Depuis 1998, le site http://www.random.org/ propose des services de génération de vrais nombres aléatoires en utilisant les fluctuations atmosphériques. Les nombres aléatoires proviennent donc d’un système chaotique et on sait que ces systèmes ne sont pas prédictibles (contrairement à un générateur de nombres pseudo-aléatoires) même s’ils sont déterministes.

D’un autre côté, la physique quantique permet aussi d’obtenir de vrais nombres aléatoires. Bien que les équations quantiques (Schrödinger ou Dirac) soient déterministes, elles portent sur des amplitudes de probabilités. La physique quantique est donc considérée comme intrinsèquement aléatoire. La société id Quantique, spécialisée dans la cryptographie quantique fournit un vrai générateur de nombres aléatoires depuis 2004. C’est un matériel que l’on peut acheter sous forme d’un composant électronique, d’une carte PCI ou d’un appareil USB externe depuis peu.

Et maintenant, à l’ère du Web 2.0, de l’architecture SOA, je viens de découvrir un nouveau service de génération de nombres aléatoires : Quantum Random Bit Generator Service.
Ce service s’appuie sur un générateur de nombres aléatoires quantique, le QRBG121. Plusieurs clients existent pour appeler ce service : en Java, en C++, en Matlab, Octave…

Suppléments :
On pourra trouver ici différentes implémentations du Mersenne Twister en Java, C++, et bien d’autres langages.

Quelques exercices pour jouer un peu avec les nombres aléatoires (et en particulier, voir comme il est difficile pour nous d’en générer) : Can You Behave Randomly? (Laissez-moi un commentaire si vous faites une séquence aléatoire. Moi, je n’ai pas réussi )

Les cinq grands problèmes de la physique théorique actuelle selon Lee Smolin :

1. Unifier la relativité générale et la physique quantique.
2. Comprendre la physique quantique.
3. Aller au delà du modèle standard de la physique des particules. En particulier, trouver une théorie expliquant toutes les particules ainsi que les différents paramètres du modèle standard (masse, constantes de couplage…)
4. Expliquer comment la nature détermine les variables du modèle standard.
5. Trouver une théorie de la matière noire et de l’énergie noire.

Les grandes directions de recherche proposées par Lee Smolin pour attaquer ces problèmes :

1. Approfondir les régularités du fond de radiation cosmologique (CMB)
2. Approfondir les différences d’accélération des étoiles dans une même galaxie (MOND)
3. Approfondir par des expériences la variabilité des constantes fondamentales (exemple des théories VSL « variable speed of light »).
4. Si la constance de la vitesse de la lumière est remise en cause, alors il faut approfondir les conséquences pour la relativité restreinte et pour la constante de Planck.
5. Approfondir la gravitation quantique à boucles (loop quantum gravity).

Source : Le blog d’Automates Intelligents » The trouble with Physics, de Lee Smolin

C’est impressionnant comment un simple dessin au tableau peut prendre vie…

Ce dessin animé explique en 5 minutes une des expériences qui montrent pourquoi la physique quantique est un casse-tête qui occupe les physiciens (et/ou philosophes) depuis plus de 80 ans.

Bien sûr, il ne faut pas prendre pour argent comptant tout ce qui y est dit. J’ai lu quelques commentaires sur Youtube qui critiquent tel ou tel passage de la video. Mais je pense que le but n’est pas d’expliquer comment se comportent les particules quantiques, mais plutôt de retracer en quelques minutes les différentes hypothèses que des physiciens, voire des philosophes, ont pu avancer pour expliquer le comportement étrange des électrons.

Pour moi, ce petit film est bien fait et donne envie de s’intéresser à ce phénomène. Bon, j’avoue, mon intérêt n’est pas nouveau

En tout cas, si on veut voir plus de scientifiques dans les universités dans les années à venir, je crois que quelques films comme ça pourrait initier quelques vocations. Après tout, les sciences ne sont pas une technologie dont on connaît les tenants et aboutissants. Les sciences sont un questionnement (et émerveillement) permanent au sujet d’un monde encore mal connu.

C’est un peu de la propagande ou de la pub, si on veut.

Les exposés de la Journée du centenaire de la mort de Ludwig Boltzmann organisée par Jacques Bouveresse le 22 novembre 2006 sont disponibles au format audio ici : Colloques – Philosophie du langage et de la connaissance – Jacques Bouveresse

J’en ai parlé ici et là.

Voici un petit article sympa dans lequel les auteurs montrent qu’un qubit (un bit quantique) peut être vu comme la généralisation matricielle du bit classique. L’article fait 4 pages. La deuxième page est suffisante pour comprendre ce que présentent les auteurs. Le reste n’est que la généralisation à dimensions.

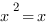Le point de départ est l’équation de Boole : qui montre que les symboles logiques peuvent s’écrire sous la forme 0 ou 1. Les auteurs généralisent l’équation à une matrice :
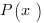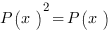avec 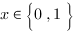un symbole logique. Cette équation est l’équation d’un projecteur (opérateur familier de la mécanique quantique).

La solution de cette équation est la matrice
.

Le lien avec la notation de Dirac est donné par
P(x)= | x >< x | avec |x > =.

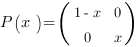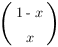On retrouve les qubits de base |0> et |1> pour les valeurs 0 et 1 de . Un qubit est donc un vecteur à 2 dimensions.

Une particule de spin 1 possède 3 états de spin et représente un qutrit (bit quantique à 3 niveaux). Cet état est représenté par un vecteur à 3 dimensions 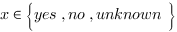dépendant de la variable logique classique – voir l’Equ. (7).

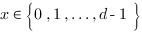En dimension , la variable logique possède donc modalités.

Je manque encore un peu de culture sur les différentes logiques, mais il me semble que cette approche est lié à la logique polyvalente. En parcourant un peu l’historique de cette logique, on voit qu’elle est apparue dans les années 20 et qu’elle a conduit aux ensembles flous (utilisés parfois pour représenter des structures quantiques) et à la logique floue.

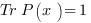Pour leurs généralisations, les auteurs utilisent toujours l’équation et l’équation de normalisation , mais l’équation de Boole n’est pas conservée. Une question que l’on peut se poser est : pourquoi conserver l’équation de Boole matricielle en dimension supérieure à 2 et pas l’équation de Boole usuelle ?

Dans un article de Physics World, D. Kaiser explique que la taille des classes infuence la façon dont la mécanique quantique est abordée. Plus une classe est remplie, moins l’enseignant se penche sur les aspects philosophiques de la mécanique quantique.

Avant la deuxième guerre mondiale, l’enseignement de la physique quantique incitait à réfléchir sur les conséquences de la théorie sur la conception du monde.

Après la guerre, les classes (surtout aux Etats-Unis) se sont remplies. On formait beaucoup de physiciens pour le nucléaire. Le but alors n’était plus de comprendre, mais de calculer. Les questions d’ordre plus philosophiques étaient plutôt des distractions par rapport à la tâche principale qui était l’approfondissement des conséquences de la théorie quantique, par le calcul. L’enseignement portait donc sur le comment et non sur le pourquoi.

Passée cette période d’après-guerre, le nombre d’étudiants en physique a commencé a chuter énormément dans les années 70. Et les aspects philosophiques laissés de côté sont réapparus dans les cours et dans les livres.

Actuellement, il y a un grand retour sur les fondements de la physique quantique. Avec les nouvelles orientations vers des aspects liés à la théorie de l’information (ordinateurs quantiques, algorithmes quantiques…), beaucoup essaient de mieux appréhender la signification de la mécanique quantique, ou de l’appréhender différemment à partir des avancées faites en théorie des probabilités, théorie de l’information…

Ainsi, on peut se poser la question d’actualité suivante : La désaffection des étudiants pour les sciences dures pourrait-elle avoir un aspect positif ?

La compagnie canadienne D-Wave a fait beaucoup de bruit en février dernier en présentant une démonstration de son ordinateur quantique appelé Orion. La présentation est disponible en pdf ici. Le processeur est composé de 16 qubits et la compagnie prévoit de passer à 1024 qubits fin 2008.

Geordie Rose, un des fondateurs de D-Wave, explique dans les colonnes de Physics World que Orion n’est pas en fait un ordinateur complètement quantique. Il est construit selon la théorie des ordinateurs quantiques adiabatiques (adiabatic quantum computers). Une des limitations de cette technologie est l’impossibilité de simuler des systèmes quantiques.

Il indique également qu’un ordinateur quantique ne saura probablement pas résoudre des problèmes NP-difficiles exponentiellement plus vite qu’un ordinateur classique.  Selon lui, le gain en vitesse pourra n’être que quadratique, ce qui serait déjà une grande avancée pour certains problèmes.

Contrairement à ce que prédisait une grande partie des chercheurs, il se pourrait bien qu’on n’attende pas 2050 pour assister à une petite révolution dans le monde des ordinateurs… D’autant plus que les algorithmes quantiques actuellement connus concernent des domaines très importants comme la cryptographie et la recherche d’information dans des bases de données.