Des interférences avec des particules
Imprimer ce billet
Source : [0809.0616] Event-by-event simulation of double-slit experiments with single photons
L’objectif de l’article est de montrer que les figures d’interférences produites par des expériences de type « fentes d’Young » peuvent être simulées par ordinateur en posant un modèle de type corpusculaire et en modélisant judicieusement les détecteurs.
Le modèle proposé est strictement local et causal et décrit complètement l’apparition d’interférences. Il s’exprime en termes de particules seulement et n’utilise ni les concepts de la mécanique quantique, ni ceux des probabilités. Les photons sont émis par une source un à un et n’ont pas d’interaction entre eux. Ils possèdent l’information de la fente par laquelle ils sont passés (encodée dans la phase)., mais cette information n’est pas utilisée directement pour la reconstruction des interférences.
Tout réside dans la modélisation du détecteur de photons qui se veut un peu plus réaliste que d’habitude. En effet, le modèle prend en compte les effets de mémoire et de seuil des détecteurs.
Les protagonistes de la simulation sont les suivants :
- Le photon
est modélisé par un vecteur à deux dimensions représentant la phase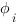 
du champ électromagnétique 
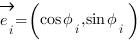. Sa phase porte l’information du temps de vol (modulo la longueur d’onde) et est calculée selon les lois de l’optique géométrique. - La source « attend » que le photon ait atteint le détecteur avant d’envoyer le photon suivant.
- Le détecteur possède un vecteur interne de polarisation
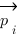de norme inférieure à 1. Ce vecteur de polarisation est mis à jour lors de la réception d’un photon par la formule 
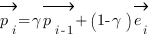. Et le signal de sortie du détecteur vaut 1 (photon détecté) lorsque le module de la polarisation est supérieur à un seuil 
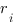, sinon 0 (photon non détecté). Le paramètre 
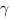contrôle la mémoire du détecteur entre chaque photon ainsi que l’effet du champ électromagnétique du photon sur le détecteur. le paramètre 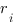est aléatoire et représente l’imprévisibilité de la réponse du détecteur.
Ces équations ne sont pas prises au hasard mais respecte la théorie de Maxwell.
Le détecteur a une extension spatiale limitée. Il en faut donc une grande quantité pour former un écran derrière les fentes d’Young.
Avec ce modèle, les auteurs reproduisent les résultats quantitatifs des expériences de la double fente, de l’interférence de deux sources et du biprisme de Fresnel.
L’accord avec les différentes expériences est obtenu avec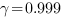 
.
Plusieurs points mériteraient probablement d’être détaillés dans l’article :
- Pourquoi cette valeur de 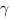, comment varient les figures d’interférences lorsque 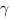varie.
- Quelle est la distribution utilisée pour le seuil 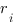? Et quelle est sont influence sur les interférences ? Faut-il nécessairement avoir un seuil aléatoire ?
- Quelle est l’extension spatiale d’un détecteur ? Que se passe-t-il lorsque l’on fait varier ce paramètre ?
Un des auteurs avait déjà proposé une simulation de l’expérience EPR reproduisant les caractéristiques quantiques à partir d’un modèle classique dans lequel le détecteur joue un rôle essentiel.
Ces modèles sont intéressants parce qu’ils montrent qu’on peut reproduire les phénomènes soit-disant typiquement quantique à l’aide de modèles réalistes simples. Ils ne remettent pas en cause la mécanique quantique mais participent à sa démystification. Cependant cela restent des modèles pour lesquels certains paramètres sont ajustés de façon à coincider avec les expériences. Il me semble que pour le moment, aucun de ces modèles ne justifie complètement les valeurs des différents paramètres.
PS: En recherchant des références pour ce billet, je suis tombé sur ce site avec des simulations visuelles d’optique ondulatoire. A visiter pour ceux qui veulent se remémorer ou simplement découvrir les différents types d’interférences.
qubits, 
étant le nombre de qubits de stockage (permettant de stocker 
enregistrements) et 
étant le nombre de qubits temporaires nécessaires pour les diverses opérations.