Le chapitre 6 traite de la relation client qui est devenue centrale pour l’entreprise ces dernières années. La GRC (Gestion des Relations Client) ou CRM (Customer Relationship Management) nécessite de définir précisément une dimension client conforme. Il existe des solutions GRC clés en main, mais celles-ci doivent s’intégrer à l’informatique de l’entreprise si on ne veut pas qu’elle devienne simplement une source supplémentaire d’informations incohérentes.
La dimension client est généralement très complexe. Elle peut être énorme : plusieurs centaines de milliers de lignes et plusieurs milliers d’attributs.
Concernant les noms et adresses, ceux-ci doivent être stockés à l’aide des « briques » les plus élémentaires possibles (par ex. : n° de rue, nom de rue, type de voie, boite postale, bâtiment…). La gestion de l’internationalisation est très complexe. Elle est traitée par Toby Atkinson dans « Merriam Webster’s Guide to International Business Communications » (Merriam-Webster, 1999).
Les clients ont également beaucoup d’attributs date (date de 1er achat, date de dernier achat, date de naissance…) qui doivent utiliser la dimension Date déjà vue, à l’aide de copies. La dimension Date jointe à la dimension Client est une dimension dite déportée, qui se justifie du fait de la taille de la dimension Client.
Parmi les attributs des clients, on trouve les attributs de segmentation (sexe, âge, score indiquant le comportement,…), les attributs représentant des faits agrégés (total des dépenses…).
Une autre dimension déportée comme la géographie peut aussi être justifiée par la relative indépendance par rapport au client. On obtient alors un modèle en flocons de neige.
Les dimensions Client sont souvent des « grandes dimensions à changement rapide ». Pour gérer ce type de dimension, on crée une ou plusieurs minidimensions, chargées de stocker les attributs variant souvent ou fréquemment analysés, comme l’âge, le salaire… Concernant les attributs variant de façon continue, comme le salaire, il faut stocker dans la minidimension des tranches de salaire seulement, quitte à laisser le salaire exact dans la table de faits. La table de faits se voit ajouter une clé étrangère pointant sur la minidimension. S’il y a besoin d’analyser les clients en fonction d’attributs de la minidimension, alors on peut faire une dimension déportée (en faisant une jointure avec la table client) en plus d’une minidimension (jointe sur la table de faits). Cependant la clé externe dans la dimension Client doit être de type 1 (i.e. écrasée à chaque changement).
Les minidimensions doivent éviter de dépasser les 100.000 lignes.
Dans le cas où les clients ont une structure hiérarchique récursive de profondeur variable, il est possible d’utiliser une table passerelle gérant les liens entre les clients.
Cette approche permet d’utiliser le SQL standard pour les groupements et cumuls, mais il est souhaitable d’utiliser des outils OLAP non relationnels pour simplifier les requêtes. « Cette approche tente de rapprocher deux structures intrinsèquement différentes, [... cela] revient à mélanger de l’huile et de l’eau. »
Source : Ralph Kimball et Margy Ross, « Entrepôts de données, guide pratique de modélisation dimensionnelle« , 2ième édition.
 Imprimer ce billet
Imprimer ce billet




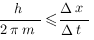 permet de montrer que les trajectoires sont continues, mais non différentiables :
permet de montrer que les trajectoires sont continues, mais non différentiables :
 est une variable aléatoire et les valeurs +1 ou -1 sont supposées équiprobables. On a donc une marche aléatoire.
est une variable aléatoire et les valeurs +1 ou -1 sont supposées équiprobables. On a donc une marche aléatoire. est markovien (
est markovien ( et
et  et
et  et non de
et non de  ), alors cette marche aléatoire équivaut à une équation différentielle stochastique usuelle.
), alors cette marche aléatoire équivaut à une équation différentielle stochastique usuelle.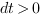 . Les variables cachées
. Les variables cachées  sont supposées différentiables par rapport au temps.
sont supposées différentiables par rapport au temps. , Smolin fait l’hypothèse d’interchangeabilité entre la limite
, Smolin fait l’hypothèse d’interchangeabilité entre la limite  et l’intégration sur les variables cachées
et l’intégration sur les variables cachées 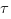 . Au-dessous de cette échelle, les trajectoires sont différentiables. Au-delà, elles sont tellement chaotiques qu’une description de la dynamique en termes d’ensemble de particules est plus appropriée.
. Au-dessous de cette échelle, les trajectoires sont différentiables. Au-delà, elles sont tellement chaotiques qu’une description de la dynamique en termes d’ensemble de particules est plus appropriée.