C’est toujours un plaisir d’écouter Alain Connes lors de ses exposés, même si je n’ai pas vraiment le niveau mathématique pour bien comprendre tout ce qu’il présente. J’essaie de présenter ci-après les notes que j’ai pu prendre durant la conférence en ajoutant quelques liens sur divers articles en rapport avec le sujet.
Mise en garde : Il se peut bien sûr que dans ces notes, des erreurs aient pu se glisser du fait de ma mauvaise connaissance de certains des domaines abordés. Je remercie l’éventuel lecteur expert qui laissera un commentaire permettant de corriger ces erreurs.
Pour cette journée sur Boltzmann, Alain Connes nous présente un lien entre la thermodynamique quantique et le temps.
Dans l’ensemble canonique, l’état de Gibbs d’un opérateur  est donné par
est donné par  .
.
Dans la représentation de Heisenberg, l’opérateur  dépend du temps :
dépend du temps :
 , où
, où  est le hamiltonien. La dynamique est donnée par un groupe d’automorphismes à un paramètre de l’algèbre des observables
est le hamiltonien. La dynamique est donnée par un groupe d’automorphismes à un paramètre de l’algèbre des observables  .
.
Le point essentiel de l’exposé est la condition KMS qui relie un état à son évolution dans le temps :


Le temps imaginaire permet l’échange de  et
et  .
.
En 1967, Tomita montre qu’il existe un unique groupe à un paramètre qui vérifie la condition KMS pour  pour une algèbre de von Neumann.
pour une algèbre de von Neumann.
Dans sa thèse en 1972, Alain Connes montre qu’une algèbre de von Neumann possède une évolution canonique. Une algèbre non commutative « tourne » avec le temps, elle a une période. La non-commutativité implique l’évolution. De la non-commutativité surgit un paramètre qui ressemble au temps.
La question que se pose Alain Connes par la suite est de savoir si cette évolution est liée au temps.
En 1992, Rovelli propose une origine thermodynamique du temps. La question devient alors : « Quelle est la notion de temps impliquée en gravité quantique ? »
Connes et Rovelli ont publié ensemble un article sur cette question.
D’après l’article de Tomita, chaque fois qu’on se donne un état, on a donc un groupe à un paramètre. En prenant comme état initial le bain thermique dans l’univers (le rayonnement à 3K), et en se rappelant notre déplacement par rapport à ce rayonnement, on note que l’invariance de Lorentz est brisée par ce déplacement. Le soleil se déplace en effet à 370km/s par rapport à ce bain thermique et notre galaxie à plus de 600km/s. (Connes fait remarquer que si ce rayonnement avait été découvert au 19ième siècle, il aurait pu être à tort pris pour l’éther.) Notre temps apparaît comme le paramètre naturel obtenu si l’on part avec l’état initial donné par le fond cosmologique.
Frobenius en caractéristique zéro et lien avec la théorie des nombres. (Désolé, je n’ai pas assez bien suivi ce passage pour le retranscrire ici).
Thermodynamique des espaces non-commutatifs (ENC).
Un ENC a une évolution dans le temps, donc un groupe à un paramètre. Il est possible de changer la température pour « refroidir » un ENC : on cherche les états KMS pour  correspond à la fonction zeta de Riemann. A son pôle
correspond à la fonction zeta de Riemann. A son pôle  correspond un système quantique.
correspond un système quantique.
KMS et la transition de phase électrofaible.
Dans le modèle standard, on a une brisure spontanée de symétrie due à un potentiel quartique (double puits) pour lequel il y a brisure de symétrie. Si la température augmente, le potentiel n’a plus qu’un puits et la symétrie est restaurée. En relativité, dès qu’on fait de la géométrie, il y a brisure de la symétrie qui permet d’échanger toutes les géométries.
Il existe un ensemble d’analogies entre les Q-Réseaux et la gravité quantique qui ne demandent qu’à être approfondies.
Alain Connes a une théorie qui redonne la gravitation quantique et le modèle standard. Elle suggère qu’il est illusoire de chercher une théorie de gravité quantique sur un seul espace-temps fixe.
Le décalage vers le rouge est une homothétie sur les fréquences, ce n’est pas une translation. Le télescope Hubble a permis d’observer un décalage d’un facteur 100.
Une image thermodynamique de la gravitation commence à se faire jour.
Pour approfondir :
Sur la condition KMS : R. Haag, N. Hugenholz and M. Winnink, Commun. Math. Phys. 5, 215 (1967).
Note : Ce résumé ne permet certainement pas de comprendre clairement ce qu’a exposé Alain Connes, mais j’espère qu’il offre tout de même quelques pistes pour étudier plus précisément le sujet.
 Imprimer ce billet
Imprimer ce billet




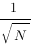 , l’inverse de la racine carrée de N (la taille de la population).
, l’inverse de la racine carrée de N (la taille de la population). est donné par
est donné par  .
. , où
, où  est le hamiltonien. La dynamique est donnée par un groupe d’automorphismes à un paramètre de l’algèbre des observables
est le hamiltonien. La dynamique est donnée par un groupe d’automorphismes à un paramètre de l’algèbre des observables  .
.

 et
et  .
. pour une algèbre de von Neumann.
pour une algèbre de von Neumann. correspond à la fonction zeta de Riemann. A son pôle
correspond à la fonction zeta de Riemann. A son pôle  correspond un système quantique.
correspond un système quantique.