Simulation numérique de l’expérience EPR-B

Voici un article « Event-by-event simulation of EPR-Bohm experiments » dans lequel les auteurs proposent une simulation numérique de l’expérience EPRB. Dans cet article, ils présentent un algorithme générant deux ensembles de données, notés permettant de retrouver la corrélation quantique en .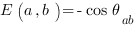
La corrélation naïve classique est linéaire et n’est pas vérifiée par l’expérience, contrairement à la relation en cosinus (provenant de la loi de Malus).
Les deux points importants de l’article sont la notion de fenêtre temporelle pour la mesure d’une coïncidence et la définition d’un instant de mesure stochastique. Les événements sur les détecteurs et interviennent en coïncidence (i.e. proviennent d’une paire de particules corrélées) s’ils ont lieu dans cette fenêtre de temps. Les variables aléatoires de spin sont corrélées classiquement (le spin 1 est opposé au spin 2). L’instant de la mesure au niveau d’un détecteur est généré aléatoirement aussi selon une distribution uniforme dans un intervalle particulier.

C’est là où je ne vois pas comment ils ont choisi cet intervalle et en particulier comment il peut être justifié. Pour l’événement n° , la particule 1, et le détecteur , l’instant de la mesure du spin est donné par une variable aléatoire dans l’intervalle
.
est un paramètre qui lorsqu’il vaut 0, permet de retrouver la corrélation linéraire du modèle naïf classique à la Bell ; et lorsqu’il vaut 3 permet d’obtenir une corrélation en cosinus telle que la corrélation quantique.

Deux mesures sur les deux détecteurs sont considérées en coïncidence si la différence entre les instants des mesures est plus petite que la fenêtre de temps choisie précédemment. Ici intervient un autre paramètre qui est la taille de cette fenêtre. La façon dont est choisi ce paramètre n’est pas claire.

Lorsque le paramètre est supérieur à 3, la corrélation est plus forte que celle prédite par la mécanique quantique. Ce paramètre semble être relié au nombre de composantes de la variable physique à décrire. Dans le cas d’un spin à trois composantes, , dans le cas d’un photon à 2 composantes, pour retrouver la corrélation quantique.

Mis à part que l’algorithme proposé reproduit les corrélations attendues par la théorie quantique et l’expérience, j’ai le sentiment qu’il manque des justifications pour les formules utilisées et les paramètres définis (d’autres articles plus détaillés semblent prévus par les auteurs).

Par contre, il ressort clairement qu’en jouant avec la temporalité des événements, on arrive à reproduire des statistiques semblables à celles obtenues par la théorie quantique. Cela me fait d’ailleurs penser à un autre exemple de simulation dans lequel une discrétisation du temps permettait de reproduire les figures interférences dans un dispositif de fentes d’Young.

L’article et d’autres références du même auteur sont disponibles ici.