[quant-ph/0609109] Could quantum mechanics be an approximation to another theory? ^[1]

Voici un article intéressant qui demande à être étudié plus en détails. Plusieurs raisons poussent l’auteur à penser que la mécanique quantique pourrait n’être que l’approximation d’une théorie plus profonde :

1. les difficultés qu’il y a à étendre la mécanique quantique à la cosmologie,
2. le problème de la mesure,
3. les succès de la théorie de l’information,
4. la « non-localité » mise en évidence expérimentalement par les expériences EPR.

L’auteur se pose la question des conditions que doit remplir une théorie cosmologique non locale qui reproduirait les résultats de la mécanique quantique. Selon Lee Smolin, une telle théorie peut être déterministe ou stochastique, mais doit certainement être non locale. Cette non-localité pourrait d’ailleurs s’expliquer à l’aide de théories microscopiques de l’espace-temps.

Pour Smolin, la dynamique stochastique de Nelson est une étape de la dérivation de la mécanique quantique à partir d’une théorie à variables cachées. Elle serait une sorte de théorie effective décrivant de façon approximative un sous-système de l’univers.

Smolin aboutit à une liste de conditions à remplir pour que la mécanique quantique soit vue comme une approximation d’une théorie non locale décrivant un sous-système :

1. Pour que le sous-système soit décrivable en termes d’équation différentielle stochastique, il faut que la moyenne faite sur les variables cachées introduise un bruit aléatoire dans l’évolution du sous-système.
2. Il doit y avoir une notion d’énergie moyenne conservée dans le temps.
3. Le système doit rester invariant par renversement du temps même après la moyene prise sur les variables cachées.
4. Les premières dérivées spatiales et temporelles sont suffisantes pour une approximation à basse énergie de la dynamique moyenne. Ce qui impose au courant de probabilité des variables du sous-système d’être irrotationnelles.

Les conditions 2 et 3 sont très contraignantes et non respectées habituellement lorsque l’on décrit un système couplé à un réservoir.

Dans le premier paragraphe, Smolin montre comment la mécanique quantique peut être retrouvée à partir de la formulation stochastique de Nelson.

Dans cette dérivation, on retrouve le potentiel quantique de la théorie de Bohm (Eq. 17). Smolin interprète de deux manières la possibilité d’obtenir la mécanique quantique à partir de la mécanique de Nelson :

• Soit on suppose que l’énergie d’une particule peut dépendre du gradient de la densité de probabilité de présence de la particule. L’ensemble statistique rentre ainsi en jeu et influence la particule (comme c’est le cas pour la théorie de Bohm).
• Soit on suppose que cette dépendance non linéaire est le résultat d’une moyenne sur une distribution de variables cachées non locales.

Smolin s’attaque à ce point dans le paragraphe suivant. Son but est de montrer que la théorie de Nelson peut à son tour être la conséquence d’une théorie à variables cachées.

Pour cela, le temps est discrétisé 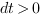. Les variables cachées sont supposées différentiables par rapport au temps.

Dans le calcul de l’énergie cinétique moyenne , Smolin fait l’hypothèse d’interchangeabilité entre la limite et l’intégration sur les variables cachées .

Cet échange de l’ordre des opérations fait passer la description de trajectoire à un point de vue ensembliste :
La notion de trajectoire non différentiable pour des particules en mouvement brownien est une bonne approximation lorsque la moyenne est faite sur une échelle de temps suffisamment grande devant l’échelle de temps microscopique 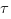. Au-dessous de cette échelle, les trajectoires sont différentiables. Au-delà, elles sont tellement chaotiques qu’une description de la dynamique en termes d’ensemble de particules est plus appropriée.

A partir de cette hypothèse de commutativité des opérations limite et intégration, l’énergie moyenne (conservée) conduisant à l’équation de Schrödinger est retrouvée (à condition d’avoir défini l’énergie cinétique de façon invariante par rapport au renversement du temps Eq. 41).

C’est seulement si l’effet des variables cachées sur les observables respecte l’invariance par renversement du temps que les équations quantiques sont retrouvées.

Concernant la théorie de Nelson : Habituellement, en mécanique statistique classique ou quantique, la moyenne d’une observable est linéaire dans la densité de probabilité. Ce n’est pas le cas dans la formulation de Nelson : l’énergie (conservée) dépend non linérairement de la densité de probabilité dans l’espace des configurations.