Voici un petit article sympa ^[1] dans lequel les auteurs montrent qu’un qubit (un bit quantique) peut être vu comme la généralisation matricielle du bit classique. L’article fait 4 pages. La deuxième page est suffisante pour comprendre ce que présentent les auteurs. Le reste n’est que la généralisation à dimensions.

Le point de départ est l’équation de Boole : 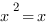qui montre que les symboles logiques peuvent s’écrire sous la forme 0 ou 1. Les auteurs généralisent l’équation à une matrice :
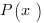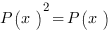avec 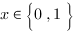un symbole logique. Cette équation est l’équation d’un projecteur (opérateur familier de la mécanique quantique).

La solution de cette équation est la matrice
.

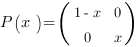Le lien avec la notation de Dirac est donné par
P(x)= | x >< x | avec |x > =.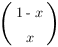

On retrouve les qubits de base |0> et |1> pour les valeurs 0 et 1 de . Un qubit est donc un vecteur à 2 dimensions.

Une particule de spin 1 possède 3 états de spin et représente un qutrit (bit quantique à 3 niveaux). Cet état est représenté par un vecteur à 3 dimensions dépendant de la variable logique classique 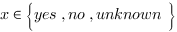– voir l’Equ. (7).

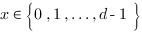En dimension , la variable logique possède donc modalités.

Je manque encore un peu de culture sur les différentes logiques, mais il me semble que cette approche est lié à la logique polyvalente ^[2]. En parcourant un peu l’historique de cette logique ^[3], on voit qu’elle est apparue dans les années 20 et qu’elle a conduit aux ensembles flous (utilisés parfois pour représenter des structures quantiques) et à la logique floue.

Pour leurs généralisations, les auteurs utilisent toujours l’équation 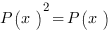et l’équation de normalisation 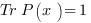, mais l’équation de Boole n’est pas conservée. Une question que l’on peut se poser est : pourquoi conserver l’équation de Boole matricielle en dimension supérieure à 2 et pas l’équation de Boole usuelle ?